목차
- Introduction
- The state of the network
- Attentive planning
- Action-plan update
- Commitment-plan update
- Learning
- Experiment
- Reference
Introduction
현재 많은 RL 논문들이 나왔고 이들은 low-level의 행동의 결과로 high-level의 행동을 이끌어내고 있지만 이 low, high level 행동의 term이 길어진다면 문제가 발생한다. 즉 sparse reward 형태가 된다면 문제가 발생한다. 그래서 이 논문은 deep recurrent neural network 구조인 STRategic Attentive Writer(STRAW)라는 구조를 제안한다. 이 구조는 macro action을 배울 수 있는 구조이다. multi-step actionplan을 가지고 있고 주기적으로 observation과 plan에 commit하여 replanning을 한다.
Straw는 두가지 모듈을 가지고 있다. 첫번째는 action plan 모듈로 macro-actions을 만드는 모듈이다. 두번째는 commit-plan을 가지고 있고 이 모듈은 언제 macro action을 끝내고 action plan을 업데이트하는 지 결정하는 모듈이다. 이 두 모듈을 업데이트하기 위해 attentive writing technique을 사용한다. 이를 통해 network가 observation의 어떤 부분을 봐야 유용한 정보를 얻을 수 있을 지 알게 해주는 기술이다.
The state of the network
t 시간에서 network의 state는 \(A^t \in R^{A \times T}\)와 \(c^t \in R^{1 \times T}\)로 이루어져있다. \(A^t\)는 action plan이다. step이 지날때마다 \(A^t\)를 shift하고 새로운 acion plan을 추가한다. \(c^t\)는 commit plan으로 언제 replanning을 할지 결정을한다. 아래는 STRAW의 schematic illustration을 보여준다.
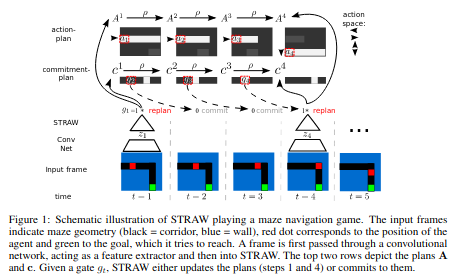 Schematic illustration fo STARW
Schematic illustration fo STARW
Attentive planning
하나의 가정으로 한 observation이 sequential action을 얻기 위해 충분한 데이터를 가지고 있다는 점이다. 그러므로 network는 최근 observation이 원하는 행동을 위해서 충분히 데이터를 가지고 있어야하므로 plan의 중요한 부분만 봐야한다. 이 논문에서는 이를 위해 attentive model을 사용한다. 보통 이미지 generation에서 사용하던 방법으로 이 논문에서는 DRAW라는 논문의 아이디어를 차용해서 사용한다.
Gaussian filter의 array를 plan에 적용하고 patch 크기로 바꾼다. 큰 Action space에서 집중하여 새롭게 만드는 것이다. A를 가능한 action 수, K를 patch 크기라고 하자. \(K \times A\) 크기의 1D gaussain filter를 사용하게된다. \(\psi\)를 grid position, stride 등과 같은 attention parameters라고 한다면 attention operations을 아래와 같이 정의한다.
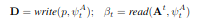
Write operation은 patch와 attention parameters를 input으로 받는다. Read operation은 action plan과 attention parameters를 input으로 받는다. 자세한 부분은 다음 section을 보면 될 것 같다.
Action-plan update
\(z_t\) feature represeation이라고 할 때 \(z_t\)와 \(g_t\)를 이용해서 STRAW는 plan update를 한다. 아래는 action-plan update의 algorithm이다.
 Algorithm1
Algorithm1
read 부분을 보면 \(A^{t-1}\)과 attention parameter input을 받아서 action plan을 생성하는 것을 볼 수 있고 이렇게 생긴 action plan과 \(z_t\)를 이용하여 patch를 생성하여 write operation을 진행하는 것을 확인할 수 있다.
Commitment-plan update
commitment-plan update는 \(c_t\)를 참고하여 \(c^{t-1}\)이 0일 경우 shift를 하고 아닐 경우 새로 replanning하여 commit plan을 update한다.
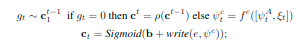
Learning
STRAW의 loss function은 아래와 같다. \(L^out\)은 A3C의 loss function이다. action plan의 raw를 이용하여 value function estimation하였다. 그리고 두번째 식은 latent distribution과 prior에 대한 kl divergence 식으로 평균 0, 분산 1 인 prior gaussian distribution에 따르도록 latent distribution을 만든다. 세번째 식은 term은 re-planning과 commitment에 관련되어 있다.
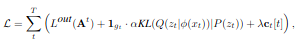
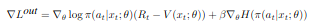
Experiment
이 논문은 2D maze를 이용하여 실험하였다. 기본적인 fully connected layer로 이루어진 방법과 LSTM, STRAW, STRAWe를 비교하였다. STRAWe는 STRAW에 gaussian noise를 더하여 exploration을 권장하는 방법이다. 실험 결과를 보면 optimal 결과인 다익스타 알고리즘 대비 STRAW가 굉장히 잘 따라가는 것을 확인할 수 있고 LSTM이 감소폭이 심한 것을 확인할 수 있다.
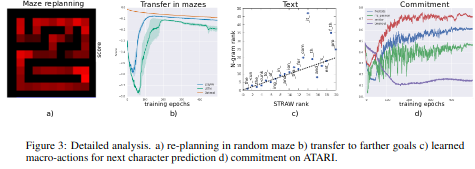 Maze Example
Maze Example
Atari 실험 결과 대부분 STRAWe가 가장 높게 나오는 것을 확인할 수 있다.
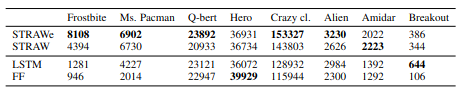 Comparison of STRAW, STRAWe, LSTM and FF baselines on 8 ATARI games
Comparison of STRAW, STRAWe, LSTM and FF baselines on 8 ATARI games
