목차
Introduction
이전 TRPO를 contraints 대신 penalty로 update하기에는 \(\beta\)를 결정하기 힘들다는 문제가 있다. 하지만 \(\beta\)를 간단하게 선택하여 업데이트 하는 방법은 policy를 최적화하기에 부족한 부분이 있다. 그래서 이 논문에서는 clip이라는 방법을 통하여 해결하고자 한다.
\[\underset{\theta}{\text{maximize}} \hat{E}_t [\frac{\pi_\theta(a_t \vert s_t)}{\pi_{\theta_\text{old}}(a_t \vert s_t)}\hat{A}_t - \beta \text{KL}[\pi_{\theta_\text{old}}(\cdot \vert s_t), \pi_\theta(\cdot \vert s_t)]]\]Clipped Surrogate Objective
기존 surrogate objective 대신 clipped surrogate objective 식은 아래로 표현된다.
\[L^{\text{CLIP}}(\theta) = \hat{E}_t [\text{min}(r_t(\theta)\hat{A}_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1+ \epsilon)\hat{A}_t)]\]clipped된 objective와 clipped되지 않은 objective 중 minimum을 사용하고 \(1-\epsilon\), \(1+\epsilon\)으로 clipped을 적용한다. objective improve가 일정 비율 이상일 경우 무시하는 방법을 적용한다.
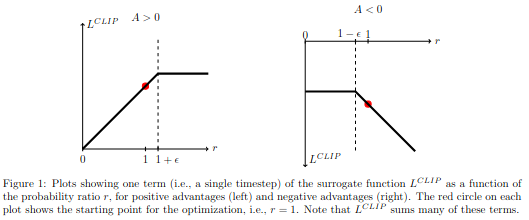 Clipped result
Clipped result
Adaptive KL Penalty Coefficient
fixed kl penalty와 clipping 방법이 아닌 새로운 방법이다. KL penalty의 값에 따라 \(\beta\)를 update하는 방법이다. clipping 대비 효과가 좋지 않지만 baseline 방법으로 생각한다.
 Adaptive KL penalty
Adaptive KL penalty
Algorithm
이 논문에서는 clipping 방법 외에 generalized advantage estimation과 entropy term을 이용한다.
Generalized Advantage Estimation
TD에서 x-step 마다 장점이 있다. x가 높을수록 variance가 낮아지고 bias가 높아지지만 x가 낮을 수록 variance가 높아지고 bias가 낮아진다. 그래서 이 모든 것을 이용하여 advantage를 생성하는 방법이 Generalized Advantage Estimation(GAE)다.:ㅈ
기존 Advantage function은 아래식으로 표현된다.
\[A^1_t = R_t + \gamma V(s_{t+1}) - V(s_t) \triangleq \delta_t\] \[A^2_t = R_t + \gamma V(s_{t+1}) +\gamma^2 V(s_{t+2}) - V(s_t)\] \[= R_t + \gamma V(s_{t+1}) - V(s_t) + \gamma(R_{t+1} +\gamma V(s_{t+2}) - V(s_{t+1}))\] \[=\delta_t + \gamma \delta_{t+1}\] \[A^n_t =\underset{k=t}{\overset{t+n-1}{\sum}} \gamma^{k-t} \delta_k\]TD는 아래 식으로 표현할 수 있다.
\[TD(\lambda) = \underset{n=1}{\overset{\infty}{\sum}} (1-\lambda) \lambda^{n-1} A^n_t\] \[=(1-\lambda)(\delta_t + \lambda(\delta_t + \gamma \delta_{t+1}) + \lambda^2(\delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2}) + \cdots)\] \[=(1-\lambda)(\delta_t(1+\lambda + \lambda^2+\cdots) + \gamma \delta_{t+1}(\lambda+\lambda^2 + \cdots) + \cdots)\] \[=(1-\lambda)(\delta_t\frac{1}{1-\lambda} + \gamma \delta_{t+1} \frac{\lambda}{1-\lambda} + \cdots)\] \[=\underset{k=t}{\overset{\infty}{\sum}} (\gamma \lambda)^{k-t} \delta_k\]Entropy
Entropy를 maximize한다는 것을 최대한 exploration을 한다는 뜻이다. 공기를 예시로 들면 entropy 개념을 잡기 편할 것이다. 공기에 열을 가하면 entropy가 높아질 것이다. 그렇다면 밀도가 낮아질 것이고 부피 내의 정보가 넓게 퍼질 것이다. 즉 RL관점에서는 exploration을 더하게된다는 뜻이다. 이부분은 이후 논문인 Soft actor critic에서 좀 더 자세히 다루면 좋을 것같다.
Experiment
no clipping or penalty, clipping, adaptive KL, fixed KL의 결과를 비교하였다. 이중에서 0.2 clipping 결과가 가장 좋을 것을 확인할 수 있다.
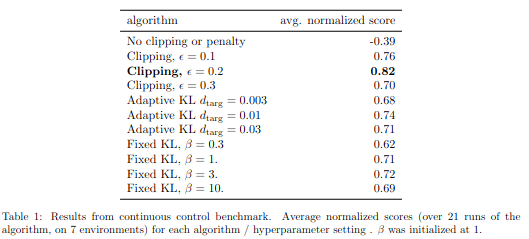 KL divergence result
KL divergence result
다른 RL 논문과 비교하였을 시 더 좋을 효과를 보여주는 것을 확인할 수 있다.
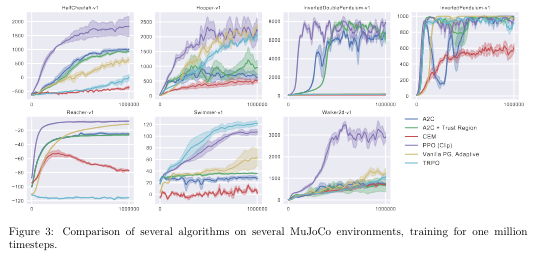 Comparing with other paper
Comparing with other paper
