목차
In previous posting
이전 posting에서 \(V(s_t)\)에 대해서 정의를 하고 이를 \(Q(s_t)\)로 표현하였다.
\(V(s_t) = \int_{a_t} Q(s_t,a_t)P(a_t \mid s_t) \, da_t\)
Assumption
\(Q=Q^*\)라면 \(P^*(a_t \mid s_t)\)만 구하면 expected return을 최대화할 수 있다.
Q에는 \(P(a_{t+1} \mid s_{t+1}), P(a_{t+2} \mid s_{t+2}) \cdots\)의 정보가 있으므로 \(Q^*\)는 \(P^*(a_{t+1} \mid s_{t+1}), P^*(a_{t+2} \mid s_{t+2}) \cdots\)를 의미한다.
\(Q(s_t,a_t) = \int_{s_{t+1}:a_{\infty}} G_t P(s_{t+1},a_{t+1} \cdots \mid s_t, a_t) \,ds_{t+1}:a_{\infty}\)
\(= \int_{s_{t+1}:a_{\infty}} G_t P(a_{t+1},s_{t+2} \cdots \mid s_t, a_t,s_{t+1})P(s_{t+1} \mid s_t,a_t) \,ds_{t+1}:a_{\infty}\)
\(= \int_{s_{t+1}:a_{\infty}} G_t P(s_{t+2},a_{t+2} \cdots \mid s_{t+1},a_{t+1})P(a_{t+1} \mid s_{t+1}) P(s_{t+1} \mid s_t,a_t) \,ds_{t+1}:a_{\infty}\)
\(= \int_{s_{t+1}:a_{\infty}} G_t P(a_{t+2},s_{t+3} \cdots \mid s_{t+1}, a_{t+1})P(s_{t+2} \mid s_{t+1},a_{t+1}) P(a_{t+1} \mid s_{t+1}) P(s_{t+1} \mid s_t,a_t) \,ds_{t+1}:a_{\infty}\)
*\(P(s_{t+1} \mid s_t, a_t), P(s_{t+2} \mid s_{t+1}, a_{t+1})\)은 transition으로 환경에서 주어지고$ \(P(a_{t+1} \mid s_{t+1})\)은 policy이다.
\(\Rightarrow\) 그러므로 \(P^*(a_t|s_t)\)를 찾는 것이 목표이다.
Optimal policy
\(Q^*\)가 최대가 되는 \(a_t\)를 고르면 \(P(a_t \mid s_t) = P^*(a_t \mid s_t)\)를 의미
\(P(a_t \mid s_t)\)= Delta function이다.
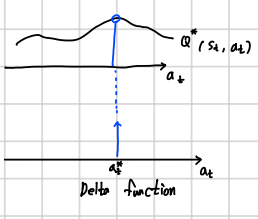
그렇다면 \(a^*_t = \underset{a_t}{\operatorname{argmax}} Q^*(s_t,a_t)\)
Greedy action(\(Q^*\)를 maximize하는 것이 가장 좋은 policy)를 하기 위해서 \(P^*(a_t \mid s_t) = \delta (a_t-a^*_t)\)이다. (\(a^*_t\)만큼 이동된 delta 함수)
*exploration 하지 않으면 optimal policy를 못찾으므로 \(\epsilon\)-greedy를 실행
