목차
Problem definition
COMA와 QMIX와 같은 논문들은 critic의 구조에 집중하여 방법론을 적용하였으며 value function에 assumption을 적용하였다는 문제가 있다. 이 논문에서는 assumption이 없고 즉각적인 intrinsic reward를 보여줄 수 있다는 장점이 있다고한다. 이 논문에서는 Intrinsic function을 이용하여 multi-agent system을 학습한다.
Background
기본적인 multi-agent system의 notation은 이전 논문들과 동일하다. 추가적으로 extrinsic, intrinsic 개념이 들어가 있다.
Extrinsic team reward
\(r^{\text{ex}}(s_t,u_t)\)Expected discounted extrinsic reward
\(J^{\text{ex}}(\pi) = E_{s_0,u_0, \cdots}[R^{\text{ex}}_0]\) with \(R^{\text{ex}}_t=\overset{\infty}{\underset{l=0}{\sum}}\gamma^l r^{\text{ex}}_{t+l}\)
Expected value function
\(V^{\text{ex}}_{\pi}(s_t) = E_{u_t,s_{t+1}, \cdots}[R^{\text{ex}}_t]\)Intrinsic reward function with parameterized by \(\eta_i\)
\(r^{\text{in}}_{\eta}(s_i, u_i)\)
The Objective
Extrinsic, Intrinsic reward를 이용하여 distinct proxy reward를 제안한다.
\[r^{\text{proxy}}_{i,t} = r^{\text{ex}}_t + \lambda r^{\text{in}}_{i,t}\]Discounted proxy reward는 아래와 같이 정의한다.
\[R^{\text{proxy}}_{i,t} = \overset{\infty}{\underset{l=0}{\sum}} \gamma^l (r^{\text{ex}}_{t+l} + \lambda r^{\text{in}}_{i,t+l})\]proxvy value function은 아래와 같이 정의한다.
\[V^{\text{proxy}}_i(s_{i,t}) = E_{u_{i,t},s_{i,t+1}, \cdots}[R^{\text{proxy}}_{i,t}]\]proxy value function \(V^{\text{proxy}}_{i}\)는 physical 의미를 가지고 있지 않다. 각 policy \(\theta\)를 update하기 위해서만 사용된다고 한다.
이 논문의 goal은 \(J^{\text{ex}}\)를 최대화하면서 proxy expected discounted return \(J^{\text{proxy}}_i\)를 최대화해서 policy parameter \(\theta_i\)를 최적화하는 것이다.
\(\underset{\eta,\theta}{\text{max}} J^{\text{ex}}(\eta)\)
\(\text{s.t.}\) \(\theta_i = \underset{\theta}{\text{argmax}} J^{\text{proxy}}{i}(\theta, \eta)\) \(\forall i \in [1,2, \cdots, n]\)
Algorithm
Goal은 bilevel optimization problem으로 policy parameter는 extrinsic expected return을 maximize하는 방향으로 update된다.
policy parameter는 아래 식을 이용하여 update된다.
\(\nabla_{\theta_i} log \pi_{\theta_i}(u_i \vert s_i) A^{\text{proxy}}_i(s_i,u_i)\)
where, \(A^{\text{proxy}}_i (s_i, u_i) = r^{\text{proxy}}_i (s_i,u_i) + V^{\text{proxy}}_{\varphi_i}(s^{'}_i) - V^{\text{proxy}}_{\varphi_i}(s_i)\)
이후 \(\eta\)를 업데이트하기 위해서 chain rule을 이용한다.
\[\nabla_{\eta_i} J^{\text{ex}} = \nabla_{\theta^{'}_i}J^{\text{ex}}\nabla_{\eta_i}\theta^{'}_i\]아래 수식은 위 수식의 앞쪽 미분 값으로 다른 parameter를 이용하여 update에 사용하기 위해서 improtance sampling을 추가해야한다.(이부분은 수식에는 안나와 있지만 algorithm에는 변경되어 표시되어 있다.)
아래 수식은 뒤쪽 미분값이다.
\(A^{\text{proxy}}_i (s_i, u_i)\)는 아래 수식으로 표현된다. 그래서 \(\eta_i\)에대해서 미분을 한다면 뒤쪽 proxy value 값은 \(\eta_i\)에 대한 수식이 아니기 때문에 사라지고 \(r^{\text{proxy}_i}\)만 남는다.(\(r^{\text{in}}_i\)만 남아야할 것같은데 논문에는 proxy로 표기 했다. 앞쪽에 \(\lambda\)가 나오고 수식상 Intrinsic return이 맞는 것 같다.)
\[A^{\text{proxy}}_i (s_i, u_i) = r^{\text{proxy}}_i (s_i,u_i) + V^{\text{proxy}}_{\varphi_i}(s^{'}_i) - V^{\text{proxy}}_{\varphi_i}(s_i)\]LIIR의 구조는 아래 그림과 같다.(마지막에 proxy와 extrinsic values의 notation 오류가 있는 것 같다.)
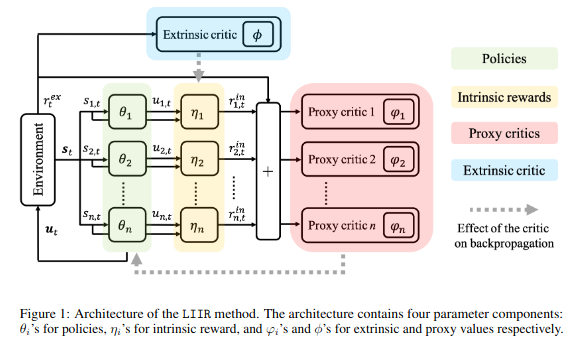 LIIR Architecture
LIIR Architecture
알고리즘은 아래와 같이 구현되어 있다.
 Algorithm
Algorithm
Experiment
간단한 게임을 이용해서 테스트를 하였다고한다. 목표 값을 설정하고 두 agent가 목표 값에 다가가는 게임으로 {+1,-1,0}의 행동을 하고 서로 다른 행동을 하면 -0.01 reward, 둘 다 좋은 행동을 하면 +0.01의 reward를 받는다. Intrinsic reward를 보면 좋은 행동을 했을 때 높은 intrinsic reward를 얻는 것을 확인할 수 있다. 또한 좋은 행동을 하는 쪽으로 학습을 하는 것을 확인할 수 있다.
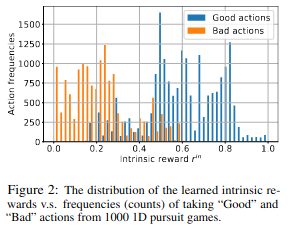 Simple game result
Simple game result
이전 논문과 동일하게 starcraft2에서 학습하였다. 다른 논문과 비교시 더 좋은 학습 결과를 얻는 것을 확인할 수 있다.
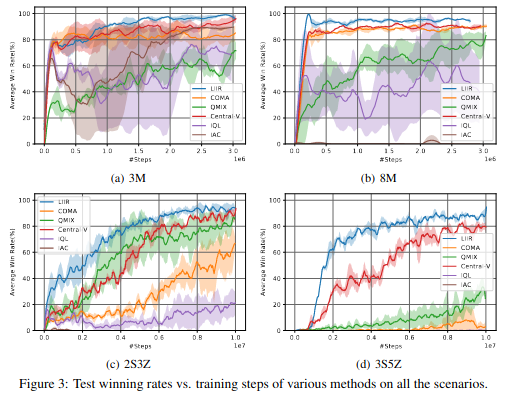 Experiment Result comparing with other method
Experiment Result comparing with other method
Intrinsic curve를 확인하면 위쪽 그림에서 캐릭터가 피가 없는 데 도망치는 것이 아닌 공격하는 판단을 하여 안 좋은 intrinsic reward를 얻는 것을 확인할 수 있고 아래 그림에서는 도망치는 판단을 하여 높은 intrinisc reward를 얻는 것을 확인할 수 있다.
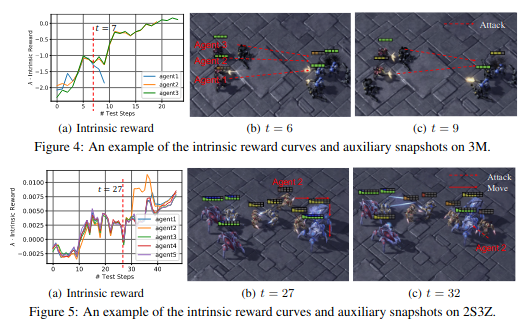 Analysis Intrinsic reward
Analysis Intrinsic reward
Code review
논문 코드를 살펴보면 Actor network에서 각 agent의 행동을 선택하고 critic network는 공용으로 사용되는 layer를 두고 Extrinsic, Proxy(mix) value function과 Intrinsic을 위해서 각각의 마지막 layer를 사용하고 있다. 또한 TD update를 위해서 TD_lambda를 사용하고 있다.
TD_lambda란 TD(1)부터 TD(\(\infty\))까지의 각각의 장점을 사용하기 위해서 모든 TD를 이용해서 expected return을 만드는 방법이다.
n=1 \(G^1_t = R_{t+1} + \gamma V(s_{t+1})\)
n=2 \(G^2_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 V(s_{t+2})\)
n=\(\infty\) \(G^{\infty}_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-1} R_T\)
TD(1)부터 TD(\(\infty\))까지 멀리까지 고려하는 TD에 discount factor \(\lambda\)를 사용하여 expected return을 생성한다. \(1-\lambda\)를 이용해서 \(\overset{\infty}{\underset{n=1}{\sum}} \lambda^{n-1}\)를 1로 되도록한다.
\[G^{\lambda}_t = (1-\lambda) \overset{\infty}{\underset{n=1}{\sum}} \lambda^{n-1} G^n_t\]왜 1-λ를 사용하는가?
위 식에서 x를 구하는 것이 목표이다. 등비 수열 공식을 이용하면 아래와 같이 \(S_t\) 표현할 수 있다.
\[S_t = \frac{x(1-\lambda^T)}{1-\lambda} =1\]T가 무한대일 경우 \(\lambda^T\)는 0에 수렴하므로 \(\frac{x}{1-\lambda} =1\)이므로 \(x = 1-\lambda\)가 나온다.
\(G^n_t\)는 TD target으로 value function을 업데이트하는 곳에 사용한다. \(G^n_t\)는 t+1의 데이터를 재귀적으로 사용하기 때문에 \(G^n_{t+1}\)로 표현할 수 있다. t=10,9,8까지 각각의 \(G^n_t\)를 표현해서 관계식을 유도해보겠다.
t=10
\(G^1_{10} = r_{11} + \gamma V(s_{11})\)
\(G^\lambda_{10} = G^1_{10}\)
t=9
\(G^1_{9} = r_{10} + \gamma V(s_{10})\)
\(G^2_{9} = r_{10} + \gamma r_{11} + \gamma^2 V(s_{11})\)
\(G^\lambda_{9} = (1-\lambda)(G^1_9 + \lambda G^2_9)\) \(=(1-\lambda)(G^1_9 + \gamma\lambda G^\lambda_{10})\)
t=8
\(G^1_{8} = r_{9} + \gamma V(s_{9})\)
\(G^2_{8} = r_{9} + \gamma r_{10} + \gamma^2 V(s_{10}) = r_9 + \gamma G^1_9\) \(G^3_{8} = r_{9} + \gamma r_{10} + \gamma^2 r_{11} + \gamma^3 V(s_{11}) = r_9 + \gamma G^2_9\) \(G^\lambda_{8} = (1-\lambda)(G^1_8 + \lambda G^2_8 + \lambda^2 G^3_8)\)
\(=(1-\lambda)(G^1_8 + \lambda (r_9 + \gamma G^1_9) + \lambda^2 (r_9 + \gamma G^2_9)\)
\(=(1-\lambda)(G^1_8 + \lambda r_9 + \lambda^2 r_9) + \gamma \lambda(1-\lambda)(G^1_9 + \lambda G^2_9)\)
\(=(1-\lambda)(G^1_8 + \lambda r_9 + \lambda^2 r_9) + \gamma \lambda G^\lambda_9\)
위 식을 일반화 하면 아래와 같이된다. \(G^\lambda_t = (1-\lambda)(\gamma V(s_{t+1}) + r_{t+1} + \lambda r_{t+1} + \lambda^2 r_{t+1} \cdots) + \gamma \lambda G^\lambda_{t+1}\)
\(= \gamma (1-\lambda) V(s_{t+1}) + (1-\lambda)\overset{\infty}{\underset{n=1}{\sum}} \lambda^{n-1} r_{t+1} + \gamma \lambda G^\lambda_{t+1}\)
\(= \gamma (1-\lambda) V(s_{t+1}) + r_{t+1} + \gamma \lambda G^\lambda_{t+1}\)
논문에서는 위 식을 이용해서 parameter update에 사용한다.
Review comment
COMA, QMIX와 다르게 더 학습을 잘해서 focusing이나 피가 없을 때 회피하는 동작을 통하여 더 학습이 잘되는 것을 확인할 수 있다. Extrinsic과 Intrinsic을 이용해서 이전 논문과 다르게 가정이 없기 때문에 더 잘되는 것을 알 수 있으나 어떤 수학적 효과를 일으켜 학습이 잘되는 지 증명이 어려운 부분이 있는 것같다. Extrinsic, Intrinsic을 이용한 single agent 논문을 찾아보고 개념과 왜 학습이 잘 이루어지는 지를 확인해야할 것 같다.
