목차
Advantage function
Advantage function은 Q-V 수식으로 이루어져있다. 수식 자체로 보면 Q 값이 평균보다 얼마나 더 좋거나 나쁜 값을 가지고 있는 지를 나타내는 function이다. 이로 인해서 더 학습이 잘되는 것이라고 볼 수 있다.
Dueling DQN
Dueling DQN의 구조는 아래 그림과 같이 생겼다. 이전 DQN과는 다르게 뒤쪽 layer가 두 개로 나누어져 있으며 \(\alpha\), \(\beta\)로 불린다. 이 두 layer를 이용해서 Q value를 생성한다.
\[Q(s,a; \theta, \alpha, \beta) = V(s;\theta, \beta) + A(s,a;\theta,\alpha)\]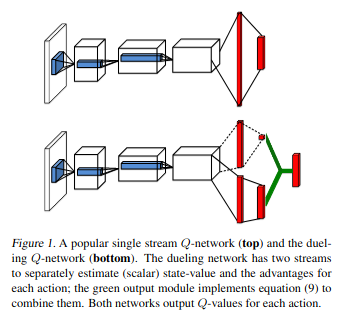
Dueling DQN Architecture
Prior information
Dueling DQN에서는 두 가지 prior information을 얘기한다.
1.A= Q-V이기 때문에 Q= A+V로 표현할 수 있다. 그리고 V = E[Q] 이므로 Q=A+V에 expectation을 넣으면 아래 수식처럼 E[A]=0이 된다.
2.deterministic policy \(a^*= \underset{a' \in A}{\operatorname{argmax}} Q(s,a')\)일 시 \(Q(s,a^*)=V(s)\)이므로 \(A(s,a^*)=0\)이 된다.
Q value with prior information
원래 Q value는 아래와 같이 정의가 되어 있다. 하지만 Advantage function은 학습을 해야하고 우리는 prior information을 가지고 있으므로 이를 이용하여 Advantage function을 더 잘 estimation하여 학습하도록 만들려고 한다.
\[Q(s,a; \theta, \alpha, \beta) = V(s;\theta, \beta) + A(s,a;\theta,\alpha)\]두번째 prior information을 이용할 경우 Q value는 아래와 같이 정의할 수 있다. maxA는 0이 되어야하므로 뒤쪽 A-maxA가 A가 되도록 의도한다.
\[Q(s,a; \theta, \alpha, \beta) = V(s;\theta, \beta) + (A(s,a;\theta,\alpha) - \underset{a' \in \vert A \vert}{\operatorname{max}}A(s,a';\theta,\alpha))\]첫번째 prior information을 이용할 경우 Q value는 아래와 같이 정의할 수 있다. 이 공식 또한 위와 같은 의미를 지닌다.
\[Q(s,a; \theta, \alpha, \beta) = V(s;\theta, \beta) +(A(s,a;\theta, \alpha) - \frac{1}{\vert A \vert} \underset{a'}{\sum} A(s,a';\theta,\alpha))\]Algorithm
Dueling DQN의 알고리즘은 아래와 같다. DDQN의 TD target을 사용하고 있으며 이전에 설명한 Q value function을 이용하여 TD target을 만든다.
Dueling DQN algorithm