목차
Introduction
anomaly detection은 high dimension data를 이용하여 low dimension으로 reduction을 하고 거기서 의미 있는 정보를 추출해야한다. 하지만 이는 suboptimal로 수렴할 수 있으며 이 문제를 해결하기 위해서 autoencoder를 이용하여 low dimension representation과 reconstruction error를 생성한다. 이러한 정보를 이용하여 guassian mixture model을 이용하여 분류를 한다. 이때 Expectation-Maximization(EM) algorithm을 사용하는 것이 아닌. Guassian distribution에 대한 probability(multi-nomial distribution)을 DNN을 이용하여 추출한다. 이를 통하여 EM algorithm을 이용하여 iterative하게 학습하는 것이 아닌 end-to-end 방식으로 한번에 학습한다.
Deep Autoencoding Gaussian Mixture Model
Anomaly detection에서는 autoencoder를 이용하여 anomal class를 구분한 연구가 많다. 대부분 정상 물질이라는 가정 하에 학습 시 이물질이 포함될 경우 이물질 또한 정상 물질로 reconstruction을 하기 때문에 이로인하여 reconstruction error가 높아진다. 이를 이용하여 anomaly detection을 실행하지만 정상 물질이 많거나 복잡한 물질의 경우 구분하기가 힘들다. 이를 위하여 이 논문에서는 Autoencoder를 기반으로한 gaussian mixture model을 제안한다. 이 모델의 구조는 다음과 같이 구성되어 있아.
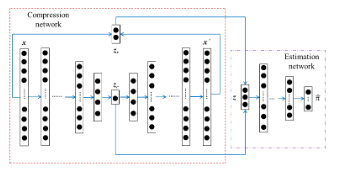 DAGMM
DAGMM
\(z_c\)는 latent vector로 input이 압축된 잠재적인 정보를 담고 있는 vector이다. latent vector는 encoder h에 의해서 생성된다.
\[z_c = h(x; \theta_e)\]reconstruction error는 input과 output의 L1, L2 norm을 이용하여 생성할 수 있다. Output은 encoder와 decoder를 지난 결과 값이다.
\[x' = g(z_c; \theta_d)\] \[z_r = f(x,x')\]reconstruction error는 L2 norm 뿐만 아니라 cos similiarity를 이용할 수 있고 이 논문에서는 latent vector, relative euclidean distiance, cosine similarity를 이용하였다.
\[z_{rel\_eucli} = \frac{\vert \vert x - x' \vert \vert_2}{\vert \vert x \vert \vert_2}\] \[z_{cos} = \frac{x \cdot x'}{\vert \vert x \vert \vert_2 \vert \vert x' \vert \vert_2}\] \[z= [z_c, z_{rel_eucli}, z_{cos}]\]End-to-end 학습을 위해서 probability를 multi-layer network를 지난 softmax결과를 사용하였다. 그래서 optimization 과정에서 expectation 과정이 줄어들어 maximization 과정만을 진행하면된다. 이 논문에서는 Gaussian mixture model의 componet를 이용하여 anomal score를 설정하고 이는 다음과 같이 정의할 수 있다.
\[\hat{\phi}_k = \underset{i=1}{\overset{N}{\sum}} \frac{\hat{\gamma_{ik}}}{N}\] \[\hat{\mu}_k = \frac{\underset{i=1}{\overset{N}{\sum}} \hat{\gamma}_{ik} z_i}{\underset{i=1}{\overset{N}{\sum}}\hat{\gamma}_{ik}}\] \[\hat{\sum}_k = \frac{\sum^N_k \hat{\gamma}_{ik}(z_i - \hat{\mu}) (z_i - \hat{\mu}_k)^T}{\sum^N_{i=1} \hat{\gamma}_{ik}}\] \[E(z) = -log(\underset{k=1}{\overset{K}{\sum}} \hat{\phi}_k \frac{\text{exp}(-\frac{1}{2}(z-\hat{\mu}_k)^T\hat{\sum}^{-1}_k (z- \hat{\mu}_k))}{\sqrt{\vert 2 \pi \hat{\sum}_k \vert}})\]DAGMM의 loss function은 다음과 같다.
\[J(\theta_e, \theta_d, \theta_m) = \frac{1}{N} \underset{i=1}{\overset{N}{\sum}}L(x_i,x'_i) + \frac{\lambda_1}{N} \underset{i=1}{\overset{N}{\sum}}E(z_i) + \lambda_2 P(\hat{\sum})\]기본적인 Anomaly detection과 동일하게 reconstruction error를 최소화 시켜주고 어떤 gaussian 분포의 평균값에 가까워지도록 학습이된다. 그리고 covariance matrics의 digonal value가 0이 되지 않기 위해서 penalty term을 추가하였다. \(\lambda_1\)과 \(\lambda_2\)는 0.1, 0.005로 각각 설정되었다.
Experiment
실험 결과는 일반적인 latent vector만을 이용한 GMM version인 GMM-EN, energy function을 제거한 버전인 PAE 등 설정에 따라 PAE-GMM-EM, PAE-GMM, DAGMM-p, DAGMM-NVI를 비교하며 실험하였다. 대부분 DAGMM이 높은 결과를 보여주었지만 DAGMM-NVI는 비슷한 결과를 보여주곤 하였다.
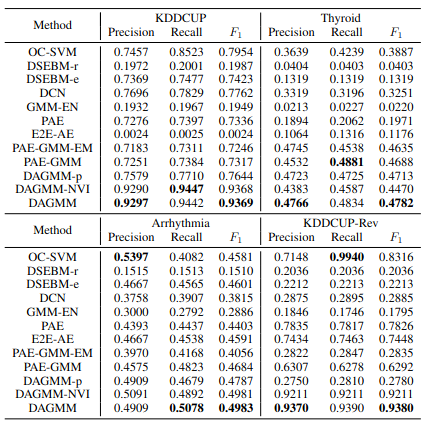 Experiment
Experiment
