목차

1. Main ideas
2. Notation
3. Indepedent Actor-Critic
4. Counterfactual Multi-Agent Policy Gradients
5. COMA Lemma 1
6. Algorithm
7. Reference

Main ideas

• Centralised critic 사용
• Counterfactual baseline 사용
• Critic representation 사용

Notation

• Stochastic game \(G = <S,U,P,r,Z,O,n, \gamma >\)
  • n agents identified by \(a \in A \equiv \{1, \cdots, n\}\)
    
  • \(s \in S\)
    
  • each agent simultaneously chooses an action \(u^a \in U\)
  • Joint action \(u \in U \equiv U^n\)
    
  • State transition function \(P(s' \mid s,u): S \times U \times S \to [0,1]\)
  • Reward runction \(r(s,u) : S \times U \to R\) and \(\gamma \in [0,1)\)
  • Observation \(z \in Z\)
  • Observation function \(O(s,a) : S \times A \to Z\)
  • Each agent has an action-observation history \(\tau \in T \equiv (Z \times U) ^*\) with conditions a stochastic policy \(\pi^a(u^a \mid \tau^a): T \times U \to [0,1]\)

Indepedent Actor-Critic

• 가장 간단하게 Multi-agent를 사용하는 방법은 agent 마다 독립된 actor와 critic을 두어 학습하게하는 방법이다.
• 이를 이 논문에서는 IAC라고 칭한다.
• 하지만 각 agent는 다른 상태 관측을 하기 때문에 agent끼리 서로 협동하는 것이 아닌 따로 행동한다.
• 이는 정보 공유가 없어서 학습하는 동안 공동의 목표로 학습하지 못한다는 결과를 보여준다.

Counterfactual Multi-Agent Policy Gradients

• 제일 처음 말했던 main idea 세 가지를 사용한 방법이다.
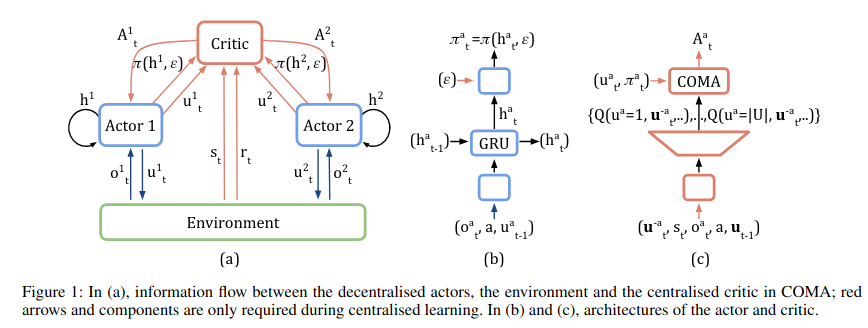
• Centralised critic
  • IAC와 달리 centralisation of the ciritic을 사용한다.
  • 이를 적용하는 방법으로 TD error를 이용하여 Update하는 방식이다.
    \(g = \bigtriangledown_{\theta^{\pi}} log\pi(u \mid \tau_t^a) (r + \gamma V(s_{t+1}) + V(s_t))\)
  • 하지만 global reward만을 고려하기 때문에 각각의 agent가 global reward에 얼마나 기여했는 지를 몰라 학습하기 위한 TD error를 만들기가 어렵다.
• Counterfactual baseline
  • 각 agent들이 shaped reward를 통해서 학습한다.
    \(D^a = r(s,u) - r(s,(u^{-a},c^a))\)
  • agent a의 action을 \(c^a\)로 대체하여 reward를 얻을 후 이를 global reward를 빼서 해당 agent의 reward를 구하는 방식이다.
  • 이 방식은 agent a의 action을 \(c^a\) default action으로 대체하여 해당 agent의 원래 action과 상관 없는 reward를 생성하여 이를 이용하는 것이 핵심이다.
  • 하지만 \(r(s,(u^{-a}, c^a))\)를 측정하기 위해서 시뮬레이터를 모든 agent에 대해서 계속 사용해야한다는 문제가 있다. 또한 \(c^a\)를 각 환경마다 선정하는 데 어려움이 있다.
  • 이렇게 구한 Q 값을 이용하여 advantage fuction을 구할 수 있다. \(A^a(s,u) = Q(s,u) - \sum_{u'^a} \pi^a(u'^a \mid \tau^a)Q(s,(u^{-a}, u'^a))\)
  • joint action을 고정시켜두고 agent a의 action의 경우의 수를 모두 구하여 value function을 구하여 advantage function을 구하는 방법이다.
• Critic representation
  • DNN을 사용할 경우 이러한 advantage function을 구하는 것이 오랜 시간(비용)이 든다.
  • 기존에는 advantage fucntion을 구하기 위해 여러번의 DNN inference를 통하여 구하였다.
  • 그래서 advantage function의 만들기 위한 정보를 입력한 후 single forward pass만으로 근사화하여 구할 수 있도록하였다.

COMA Lemma 1

• 알고리즘이 최적의 policy를 찾는 것을 보여주기 위해서는 해당 수식이 convergence를 보여주면 된다.
  \(g_k = E_\pi [\sum_a \bigtriangledown_\theta log\pi^a(u^a \mid \tau^a) A^a(s,u) ]\)
  \(A^a(s,u) = Q(s,u) - b(s,u^{-a})\)

• 우선 \(g_b\)만을 고려
  \(g_b = -E_\pi [\sum_a \bigtriangledown_\theta log\pi^a(u^a \mid \tau^a)b(s,u^{-a})]\) \(g_b = - \sum_sd^\pi(s) \sum_a\pi(u \mid \tau) \bigtriangledown_\theta log\pi^a(u^a \mid \tau^a)b(s,u^{-a})\) \(= - \sum_sd^\pi(s) \sum_a\sum_{u^{-a}}\pi(u^{-a} \mid \tau -a) \sum_{u^a}\pi^a(u^a\mid \tau^a) \bigtriangledown_\theta log\pi^a(u^a \mid \tau^a)b(s,u^{-a})\) \(= - \sum_sd^\pi(s) \sum_a\sum_{u^{-a}}\pi(u^{-a} \mid \tau -a) \sum_{u^a}\pi^a(u^a\mid \tau^a) \frac{\bigtriangledown_\theta \pi^a(u^a \mid \tau^a)}{\pi^a(u^a \mid \tau^a)} b(s,u^{-a})\)
  \(= - \sum_sd^\pi(s) \sum_a\sum_{u^{-a}}\pi(u^{-a} \mid \tau -a) \sum_{u^a} \bigtriangledown_\theta \pi^a(u^a \mid \tau^a)b(s,u^{-a})\)
  \(= - \sum_sd^\pi(s) \sum_a\sum_{u^{-a}}\pi(u^{-a} \mid \tau -a) \bigtriangledown_\theta \sum_{u^a} \pi^a(u^a \mid \tau^a)b(s,u^{-a})\)
  \(= - \sum_sd^\pi(s) \sum_a\sum_{u^{-a}}\pi(u^{-a} \mid \tau -a) \bigtriangledown_\theta b(s,u^{-a})\)
  \(= - \sum_sd^\pi(s) \sum_a\sum_{u^{-a}}\pi(u^{-a} \mid \tau -a) b(s,u^{-a}) \bigtriangledown_\theta 1\)
  \(=0\)

• \(g_b\)는 0의 값을 가지므로 variacne를 낮춰주긴하지만 expected gradient에는 영향이 없다.
• 그렇다면 \(g\)의 앞쪽의 Q function만 있는 부분을 보자.
  \(g= E_\pi [\sum_a \bigtriangledown_\theta log\pi^a (u^a \mid \tau^a) Q(s,u)]\)
  \(= E_\pi [\bigtriangledown_\theta \sum_a log\pi^a (u^a \mid \tau^a) Q(s,u)]\)
  \(= E_\pi [\bigtriangledown_\theta log \prod_a \pi^a (u^a \mid \tau^a) Q(s,u)]\)
  \(\pi(u \mid s) = \prod_a \pi^a(u^a \mid \tau^a)\)
  \(g = E_\pi[\bigtriangledown_\theta log \pi(u \mid s) Q(s,u)]\)
• 해당 공식은 single action에서 actor-critic 알고리즘에서 convergence를 증명한 공식이다.
• 그러므로 COMA의 \(g\)는 convergence하고 local optimal policy를 찾을 수 있다.

Algorithm

Reference

1. Foerster, Jakob, et al. “Counterfactual multi-agent policy gradients.” Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 32. No. 1. 2018.