목차

1. Introduction
2. Natural gradient using Kronecker-factored approximation
3. Reference

Introduction

이 논문은 TRPO에서 파생되었다. 이 논문의 주된 contribution은 TRPO의 computation time과 sample efficiency를 해결하기 위해 Kronecker-factored approximation을 사용한다는 것이다. 저자는 처음으로 scalable trust region natural graident method를 사용했다고 하는 데 이와 비슷한 ACER라는 논문이 같은 해에 나왔다.

Natural gradient using Kronecker-factored approximation

이 논문은 Kronecker-factored approximation만 알면 끝나는 논문이다. 최근 Kronecker-factored approximate curvature(K-FAC)라는 방법은 Kronecker-factored approximation을 Fisher matrix를 효율적으로 natureal gradient update를 근사하기 위해 사용되었다.

Fisher information matrix는 아래와 같이 표현된다.

\[F_\theta = E_{(x,y)}[\nabla log p(y \vert x;\theta) \nabla log p(y \vert x; \theta)^T]\]

loss function은 아래와 같이 표현된다.

\[L = E_{(x,y)} [- log p(y \vert x; \theta)]\]

이 loss function의 hessian matrix와 FIM의 상관관계는 아래와 같다.

\(H(L) = \nabla^2 E_{(x,y)} [-log p(y \vert x;\theta)]\) \(= - E_{(x,y)} [\nabla^2 log p(y \vert x;\theta)]\) \(= - E_{(x,y)} [-\frac{\nabla p(y \vert x;\theta) \nabla p(y \vert x; \theta)^T}{p(y \vert x;\theta)^2} + \frac{\nabla^2 p(y \vert x;\theta)}{p(y \vert x;\theta)}]\) \(=F_\theta - E_{(x,y)} [\frac{\nabla^2 p(y \vert x;\theta)}{p(y \vert x;\theta)}]\)

Natural Gradient Descent(NGD)의 update 공식은 아래와 같다.

\[\theta = \theta - \epsilon F^{-1}_{\theta} \nabla E(\theta)\]

이 NGD를 approximation하는 방법은 3가지이다.

1. FIM approximation
2. Reparameterize FIM
3. approximate the natural gradient directly

K-FAC는 1번 FIM approximation하는 방법이다.

K-FAC는 kronecker factorization 방법을 사용한다. 아래 그림은 kronecker factorization의 예시이다. A의 element에 B라는 matrix를 곱하는 식이다.

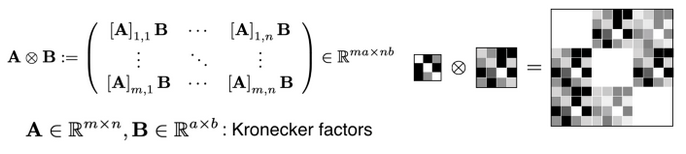Kronecker Factorization

여기에 K-FAC의 property를 적용한다.

\[(A \otimes B)^{-1} = A^{-1} \otimes B^{-1}\]

이 공식을 이용하여 approximation을 하게된다.

i-th layer의 fisher block은 아래 식으로 표현이 가능하다.

\[F_i = E[\nabla_i log p(y \vert x;\theta) \nabla_i log p (y \vert x;\theta)^T]\]

여기서 \(\nabla_i log p(y \vert x;\theta)\)는 kronecker factorization으로 approximation이 가능하다.

\[\nabla_i log p(y \vert x;\theta) = g_i \otimes a_{i-1} \in R^{d_{i=1} \cdot d_i}\]

where \(a_{i-1} \in R^{d_{i-1}}\), \(g_i= \frac{ \partial log p(y \vert x;\theta)}{\partial s_i} \in R^{d_i}\)

그래서 FIM은

\[F_i = E[\nabla_i log p(y \vert x;\theta) \nabla_i log p(y \vert x; \theta)^T]\] \[= E[(g_i \otimes a_{i-1}) (g_i \otimes a_{i-1}^T)]\] \[= E[(g_i \otimes a_{i-1}) (g^T_i \otimes a^T_{i-1})]\] \[=E[g_i g^T_i \otimes a_{i-1} a^T_{i-1}]\] \[=E[g_i g^T_i] \otimes E[a_{i-1} a_{i-1}^T]\]

K-FAC를 통하여 FIM을 approximation을 하였고 이를 통해 RL에서 variance가 낮아지는 효과를 보인다고 한다. 그래서 sample trajectory를 더 좋게 사용하여 빠르게 optimum에 가까워진다고 말하고 있다.

Reference

1. Wu, Yuhuai, et al. “Scalable trust-region method for deep reinforcement learning using kronecker-factored approximation.” arXiv preprint arXiv:1708.05144 (2017).
2. Kronecker-factored approximation curvature