목차
Introduction
학습을 위해서 Sampling을 하는 것은 중요하지만 좋은 효과를 보기 위해서는 많은 sampling을 해야한다는 문제가 있다. 그래서 가지고 있는 sample을 효율적을 사용하는 게 중요하다. 해당 논문에서는 이 문제를 해결하기 위해서 importance weight을 수정하는 방법을 제안한다. Importance sampling은 sample efficient를 위해서 많이 사용되지만 불안정하고 오히려 값을 나누게 되면서 unbound하기 때문에 문제가 발생할 수 있다.
Discrete Actor Critic With Experience Replay
Importance weight를 사용하게 되면 unbias하지만 높은 variance가 문제다. 이는 unbounded importance weight 때문인데 이 논문에서는 clipping을 통하여 해결하였다. 이 논문에서는 truncation technique이라고 얘기한다.
다른 논문에서는 marginal value function을 이용하여 접근하였다. 그 식은 아래와 같다.
\[g^{\text{marg}} = E_{x_t \sim \beta, a_t \sim \mu}[\rho_t \nabla_\theta log \pi_\theta (a_t \vert x_t) Q^\pi (x_t, a_t)]\]여기서 중요하게 보아야할 부분은 두가지이다. 첫번째는 이 식이 \(Q^\pi\)를 알아야한다는 것이고 두번째는 product of importance weight가 아닌 marginal importance weight를 얻어야한다는 것이다.
위 식에서는 \(Q^\pi\)를 얻기 위해서는 labmda returns을 사용한다.
$R^\lambda_t = r_t + (1-\lambda)\gamma V(x_{t+1}) + \lambda \gamma \rho_{t+1} R^\lambda_{t+1}$$
Multi-Step Estimation of the State-Action Value Function
이 식에서는 \(Q^\pi\)를 얻기 위해 Retrace라는 방법을 사용한다.
\[Q^{\text{ret}}(x_t, a_t) = r_t + \gamma \bar{\rho_{t+1}} [Q^{\text{ret}}(x_{t+1}, a_{t+1}) - Q(x_{t+1}, a_{t+1})]+ \gamma V(x_{t+1})\]where \(\bar{\rho_t}\) is the truncated improtance weight, \(\bar{\rho_t}=min\{c, \frac{\pi(a_t \vert x_t)}{\mu(a_t \vert x_t)}\}\)
이를 위해서 Value function을 사용하는 것이 아닌 Q function을 사용하고 이를 이용해 value function을 estimation한다.
이 논문에서는 \(Q^{\text{ret}}\)를 이용하여 \(Q^\pi\)를 얻는다.
\[(Q^{\text{ret}}(x_t, a_t) - Q_{\theta_v}(x_t, a_t)) \nabla_{\theta_v} Q_{\theta_v}(x_t,a_t)\]Importance Weight Truncation With Bias Correction
Marignal importance weight는 커질 수 있고 불안정함이 발생할 수 있다. 그래서 importance weight를 truncate하는 correction term을 제안한다.
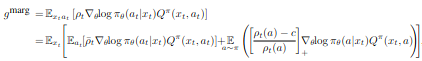Importance weight truncation with bias correction
첫번째 term은 variance를 bound되게 만든다. 그리고 correction term은 unbiased를 하도록 한다. 두번째 식의 두번째 term이 bias correction term이다. \(\rho_t(a)\)가 c 보다 작으면 0이 되고 아무리 커도 1이된다. c를 높게 설정해서 variance가 높을 경우에만 효과를 보이도록 설정하였다.
Efficient Trust Region Policy Optimization
이 논문에서는 TRPO를 이용하였는 데 TRPO의 문제인 Fisher-vector product를 매번 업데이트를 할 때마다 구해야하는 문제가 있다. 이는 높은 computation cost를 유발하는 문제가 있다. 그래서 average policy network를 제안한다. Update되는 policy가 이전 policy들의 average에 크게 벗어나지 않도록하는 방법이다.
policy network를 두 파트로 분류를 하였다. distribution f와 \(\phi_\theta(x)\)를 만드는 DNN이다.
Averaged policy network가 주어진 상태에서 이 논문의 trust region update는 두가지 stage를 가진다.
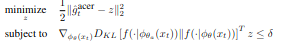
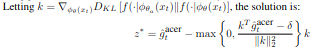
Algorithm
Algorithm